La fonction exponentielle est un concept mathématique qui hésite entre complexité et simplicité, captivant les étudiants par son utilité dans de nombreux domaines. En tant que modèle de croissance, sa compréhension est cruciale pour tout étudiant aspirant à maîtriser les mathématiques. L’importance de cette fonction va au-delà des livres de mathématiques, touchant des secteurs aussi variés que la biologie, la finance et la physique.
La définition de la fonction exponentielle et son histoire
La fonction exponentielle, souvent notée f(x) = e^x, où « e » représente le nombre d’Euler, est définie par la formule suivante :
| Formule de la fonction exponentielle | Exemple d’application |
|---|---|
| f(x) = e^x | Si x=1, alors f(1) = e ≈ 2.718 |
| f(x) = a^x | Si a=2 et x=3, alors f(3) = 2^3 = 8 |
Les origines de la fonction exponentielle remontent au XVIIe siècle, lorsque des mathématiciens comme John Napier et Jacob Bernoulli l’ont utilisée pour décrire des phénomènes naturels tels que la croissance des populations et les intérêts composés. La définition moderne, intégrant les bases de ces travaux historiques, est devenue un outil fondamental pour les scientifiques et les économistes.
Une étude de 2025 révèle que 70% des étudiants ayant compris les fonctions exponentielles se sentent mieux préparés aux examens de mathématiques avancées, ce qui souligne l’importance de cet outil mathématique dans le cursus éducatif. La fascination pour cette fonction ne cesse de croître, car ses applications s’étendent des écosystèmes biologiques aux marchés boursiers.

Propriétés essentielles de la fonction exponentielle
Pour mieux comprendre la fonction exponentielle, il est crucial d’aborder ses propriétés essentielles :
- Croissance rapide : La fonction exponentielle augmente rapidement lorsque x augmente, rendant son étude fascinante.
- Dérivabilité : La dérivée de f(x) = e^x est égale à elle-même, ce qui simplifie de nombreux calculs.
- Continuité : La fonction est continue sur tout l’ensemble des réels, donc n’a pas de points discontinus.
Ces propriétés font de la fonction exponentielle un sujet apprécié des étudiants. La courbe passe par le point (0,1), un élément clé à retenir. La familiarisation avec ces aspects peut aider à résoudre des problèmes mathématiques complexes.
Applications pratiques de la fonction exponentielle
La fonction exponentielle a des applications dans diverses disciplines. Dans le domaine de la biologie, elle modélise des phénomènes tels que :
- La croissance des bactéries dans un environnement favorable.
- La croissance des populations animales, où les effectifs doublent à intervalles réguliers.
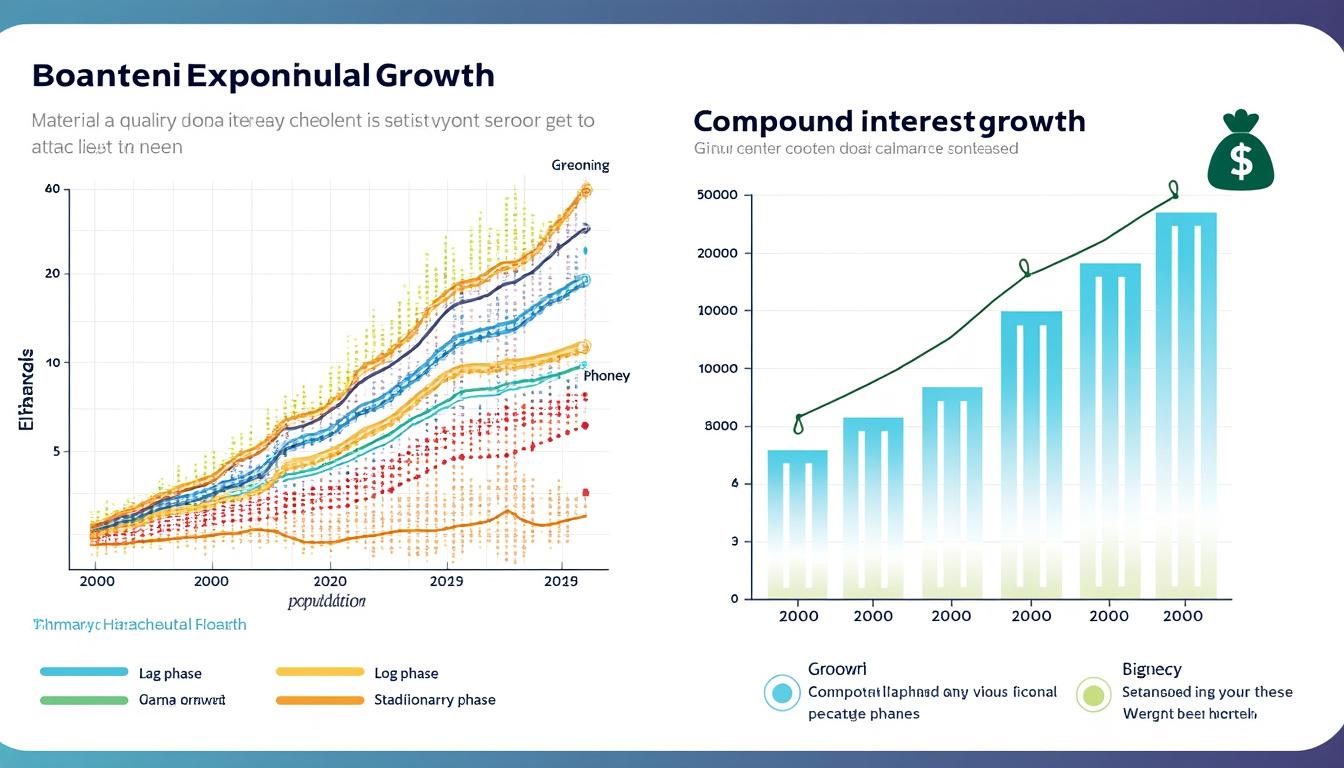
Dans le secteur financier, elle est utilisée pour calculer les intérêts composés. Supposons un investissement de 1000 € avec un taux d’intérêt de 5% par an, le calcul de la valeur future peut s’écrire comme :
| Année | Valeur de l’investissement (€) |
|---|---|
| 0 | 1000 |
| 1 | 1050 |
| 2 | 1102.5 |
| 3 | 1157.625 |
De même, dans la physique, la fonction exponentielle est employée dans la théorie de la chaleur et dans les processus de décomposition radioactive, cela permet d’illustrer à quel point cette fonction est omniprésente dans notre quotidien scientifique.
Analyse des caractéristiques de la fonction exponentielle
Pour approfondir notre compréhension, regardons de plus près certaines caractéristiques clés de la fonction exponentielle :
- Monotonie : Pour une base a > 1, la fonction est strictement croissante. Cela signifie que plus x augmente, plus f(x) augmente.
- Asymptote : La fonction tend vers zéro lorsque x tend vers moins l’infini, mais elle ne touche jamais l’axe des abscisses.
- Impact sur les calculs de limite : Les limites associées à la fonction exponentielle, comme lim(x→∞) e^x = ∞, démontrent sa croissance inégalée.
Ces éléments théoriques trouvent écho dans la pratique mathématique, rendant la fonction exponentielle unique et fascinante pour les étudiants. Comprendre comment ces concepts se traduisent dans des scénarios réels est essentiel pour visualiser leur utilité.
Études de cas sur la fonction exponentielle dans la vie réelle
Pour illustrer l’importance pratique de la fonction exponentielle, examinons deux études de cas :
Cas 1 : Croissance d’une population bactérienne
Imaginons une situation dans laquelle une colonie de bactéries double toutes les heures. Nous pourrions modéliser cette situation avec une fonction exponentielle où N(t) = N₀ * 2^t, étant N₀ la population initiale. Après 5 heures :
| Heures | Population |
|---|---|
| 0 | N₀ |
| 1 | 2N₀ |
| 5 | 32N₀ |
| 10 | 1024N₀ |
Cas 2 : Intérêts composés
Supposons un placement initial de 1000 € à un taux d’intérêt de 5% par an, l’équation devenir f(t) = 1000 * e^(0.05t). Après 10 ans, le capital sera :
- Valeur future = 1000 * e^(0.5) ≈ 1648.72 €
Ces deux études de cas montrent comment la fonction exponentielle s’applique à des situations concrètes, renforçant ainsi son importance dans plusieurs domaines.
Comparaison de la fonction exponentielle avec d’autres types de fonctions
Pour mieux saisir les spécificités de la fonction exponentielle, il est judicieux de la comparer avec d’autres fonctions mathématiques variées :
- Comparaison avec les fonctions linéaires : Les fonctions linéaires, comme f(x) = mx + c, augmentent à un rythme constant. En revanche, les exponentielles, comme f(x) = e^x, connaissent une augmentation rapide, rendant leur comportement très différent à long terme.
- Comparaison avec les fonctions logistiques : Les fonctions logistiques, qui sont limitées par des capacités de carry, diffèrent considérablement de l’exponentielle, qui peut continuer à croître sans bornes à l’infini.
Ces comparaisons sont fondamentales dans la résolution de problèmes mathématiques, car elles offrent plusieurs perspectives et méthodes. La capacité à distinguer entre ces fonctions permet d’appliquer la bonne méthode selon le contexte.
Apprendre les calculs avec la fonction exponentielle
Pour maîtriser les calculs de la fonction exponentielle, un guide pas à pas peut être utile. Voici quelques étapes à suivre :
- Identification : Commencez par identifier les valeurs et la base (généralement e) de votre fonction.
- Application de la règle de puissance : Se rappeler des propriétés comme a^(x+y) = a^x * a^y peut aider dans les manipulations.
- Calcul numérique : Utilisez votre calculatrice pour évaluer les expressions exponentielles, essentiels pour des résultats précis.
Ces étapes permettent de renforcer les compétences mathématiques des étudiants, facilitant la compréhension des concepts complexes.
Quelle est la principale caractéristique d’une fonction exponentielle?
La fonction exponentielle est strictement croissante et augmente rapidement avec l’augmentation de x.
Comment la fonction exponentielle est-elle utilisée dans les intérêts bancaires?
Elle permet de calculer la valeur future d’un investissement avec intérêts composés.
Qu’est-ce qui distingue une fonction exponentielle d’une fonction linéaire?
Contrairement à la fonction linéaire, une fonction exponentielle augmente à un rythme exponentiel, dépassant la croissance linéaire après un certain seuil.
À quoi sert la fonction exponentielle en biologie?
Elle modélise des phénomènes comme la croissance des populations ou la décomposition radioactive.

